Update
A video tutorial is now available!
If you’re using Notion then you probably know that you can’t embed HTML widgets directly into it. I have done some research and I found 2 tools that let you do so.
- htmlsave which is great but only gives you one widget for free and you have to subscribe to add more
- The potion shop is also great and has no limits on the number of widgets but adds an ad link to your widgets that just bugged me!
In this tutorial, I’ll show you how you can have as many HTML snippets on your Notion page or template as you want and without any extra ads.
step 1 : Make a GitHub repo
First of all, You’ll need a GitHub account if you don’t have one already then just create a new one.
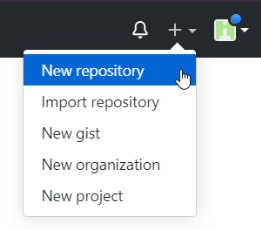
Once you have your account, go to your profile and click the plus button in the top right corner and choose “New repository”
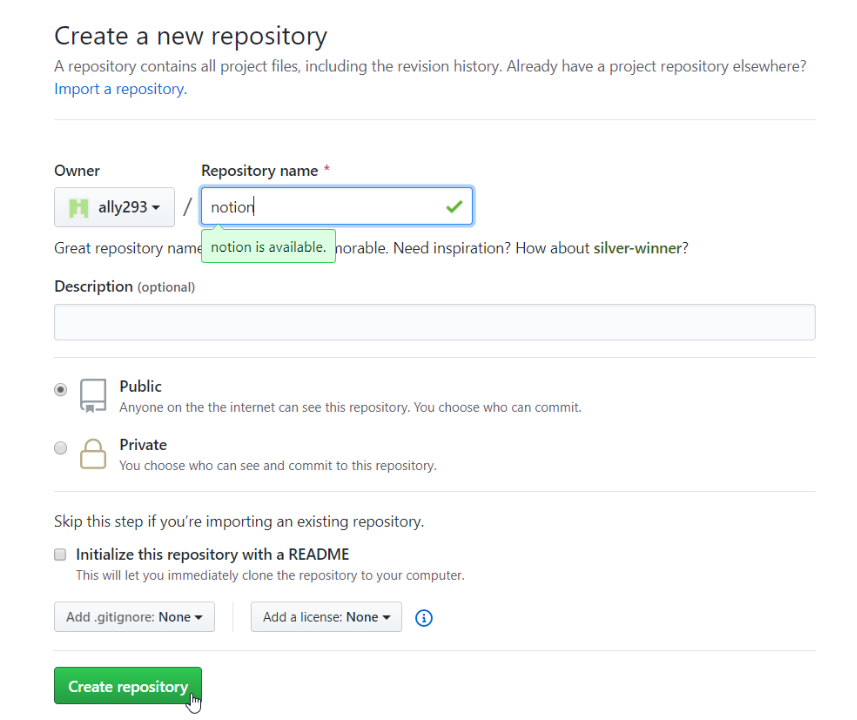
Give your repository a meaningful name and click “Create repository”. You don’t need to change anything else.
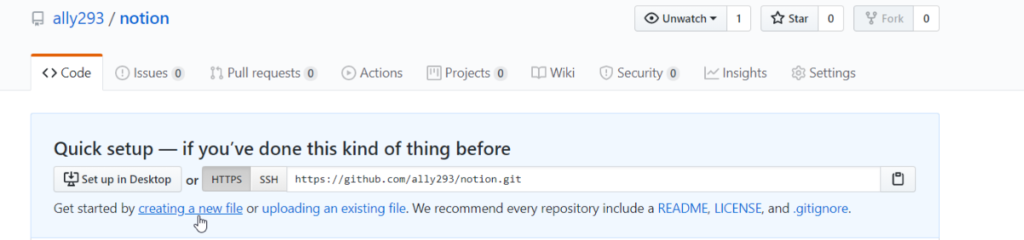
Step 2: Create your first widget
Now click on “creating a new file” to start adding your first widget/snippet.
I’m using weatherwedgit.io to get the HTML code for a nice-looking weather widget. Customize your widget as you like and then copy the HTML code and paste it into the new file you’ve just created in Github. and name the page “index.html”
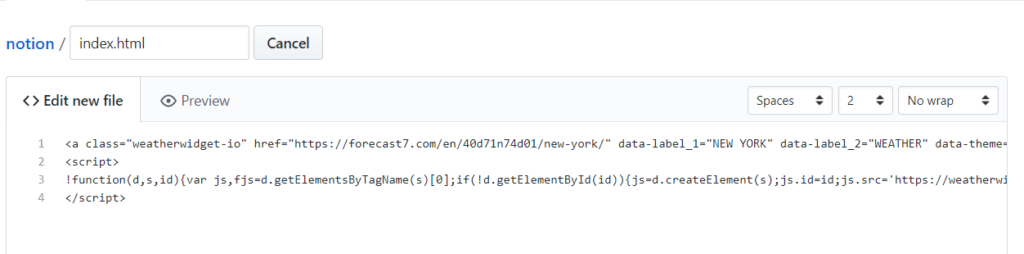
and then click “Commit changes” at the end of the page
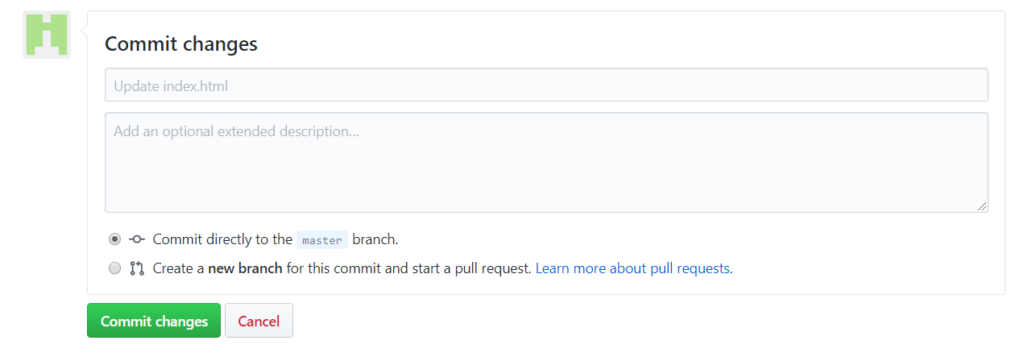
Step 3: Publish your widget
On your repository page click “settings”

Go all the way down till you find “GitHub Pages”. and choose “master branch”
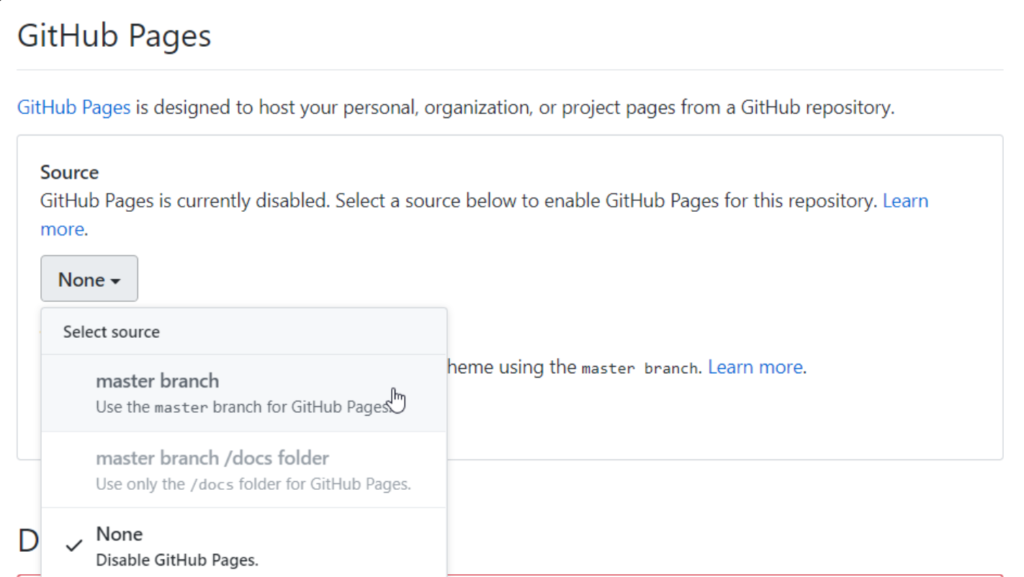
After that, click “choose a theme” and select anyone. it won’t matter.
You’ll notice now that your HTML file is published at the given link
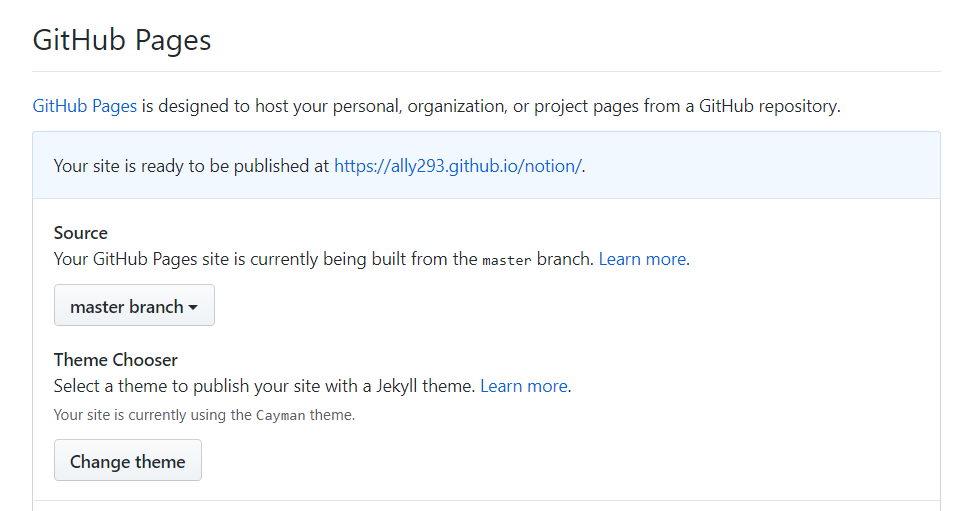
If you copied everything right then you should see the widget when you click the link.
Step 4: Adding it to Notion and creating more widgets
Copy that link and embed it as a URL into your Notion page and Voila!

Now, let’s add another widget. The widget on the left is a custom-made one that changes the greeting according to the time of day and shows the date. I’ll show you how you can add it. or, of course, you can use any other HTML snippet you want.
let’s go back to our repository and click “Create new file”

I’ll call this file “greetings.html”. whatever you wanna call it remember the name because we’re gonna use it later.
Copy and paste the following code into your newly created file
<html>
<head>
<title>Greeting Message</title>
<style>
#lbl {
font-family: monospace;
font-size: xx-large;
color: #626262;
padding: 5px;
border: 1px solid #ececec;
text-align: center;
line-height: 1.5;
height:85%
}
#date{
font-size:large;
}
body{
background-color: aliceblue;
}
</style>
</head>
<body>
<div id="lbl"></div>
</body>
<script>
var weekday = new Array(7);
weekday[0] = "Sunday";
weekday[1] = "Monday";
weekday[2] = "Tuesday";
weekday[3] = "Wednesday";
weekday[4] = "Thursday";
weekday[5] = "Friday";
weekday[6] = "Saturday";
var today = new Date();
var hrs = today.getHours();
var dayOfWeek = weekday[today.getDay()];
var date = dayOfWeek+" " + today.getDate() + "/" +(today.getMonth()+1) +'/'+today.getFullYear() ;
var greet;
if (hrs < 12)
greet = 'Good Morning ';
else if (hrs >= 12 && hrs <= 17)
greet = 'Good Afternoon ';
else if (hrs >= 17 && hrs <= 24)
greet = 'Good Evening ';
document.getElementById('lbl').innerHTML =
greet+=`<div id="date"> It's ${date}</div>`;
</script>
</html>you can personalize it more by adding your name for example. you can do so by editing that line of code
greet+=`<div id="date"> It's ${date}</div>`;to be like this
greet+= "Your name here " +`<div id="date"> It's ${date}</div>`;After you’re done, click “Commit new file”.
Your new widget link will be “your repository URL”/”your file name”. your repository URL is the one you used the first time. you can get it from the Settings under GitHub pages. Mine looks like this https://ally293.github.io/notion/greetings.html
Like you did with the first widget embed that link and you’re done!
Add as many snippets as you want. “GitHub pages” is totally free without any distracting links!”
Want some ideas for Notion widgets?
check out my 100% free Notion Widgets Gallery.







Hi,
I’m getting this when i try to view the new widget page:
File not found
The site configured at this address does not contain the requested file.
If this is your site, make sure that the filename case matches the URL.
For root URLs (like http://example.com/) you must provide an index.html file.
Read the full documentation for more information about using GitHub Pages.
Any help would be appreciated!
Thanks
I solve it!
Thanks Awesome tutorial!
Thank you! Glad you did!
Some times it just takes a few minutes for the page to go online.
Hey!
How did you solve it? I’m having the same problem.
How did you solved it?
try making an empty commit. (just add a new line to the file and commit it) that usually solves it
When I click on the link, it just brings me to the template I don’t actually see the widget.
Which link exactly? could you elaborate more, please?
Hi, I’m getting the same thing. I tried to /embed the link that is generated after selecting a theme. All this does is open a widget that views the theme preview, not the actual widget. It seems like selecting the widget does affect this. Do you have any tips for how to work around this?
I can’t make the link for the greeting 🙁
What sort of errors are you getting so I can help?
This is an amazing tutorial! Thanks!!
You’re very welcome!
When I embed the widget I get a white fram in notion, any Idea on how to fix it?
What about when you open the link in the browser does it work then? or also gives you a white page?
Thanks for the tutorial. I did it. I’m not from a computer science background, I feel invincible now😆
That awesome 😄 you can do so much more now!
It works like a charm. Cheers.
I can’t access GitHub pages without subscribing 🙁
subscribing to what?
Github premium, It’s ok through I solved it thank you!
I am truly enjoying your site! Thank you for posting so many helpful guides!!
I copied it and it worked! But then I tried to make another greetings widget by adding a file and I only see the background of the box, the time and the reminders don’t show up. Please help!
send me the link of your widget so I can help
It doesn’t work for me, Idk why but I don’t have the master branch option, there’s only one it’s called main. So the rest of the process doesn’t work neither ;(
Github renamed the “master” branch to the “main” branch so they’re basically the same thing
Great tutorial, thank you for posting! It was just what I was looking for because I didn’t want to rely on third party widgets. And now I’ve created 5 of my own – one based on your countdown. I think I’m addicted.
You’re very welcome! So glad I could help.
Hello!
I want to try to publish webgl Unity build to my Notion. Found your article, thanks. But I can`t see any pictures in this from the first step to the end. I got link like that, is it ok?
data:image/gif;base64,R0lGODdhAQABAPAAAMPDwwAAACwAAAAAAQABAAACAkQBADs=
I managed to publish and run a test draft build, but I have difficulties uploading files over 25MB, researching the issue.
How do I do this for your cooking timer? The one that you published in your Notion template? I want that one but I want to change the colors. Can you provided detailed instructions on how to host it on my own github repository? I’m a beginner and don’t really understand github. Thanks!
Thank you so much! I was desperate looking for something like this that is free, everywhere else makes you pay a subscription like html save and I don’t like that. You’re awesome!
Hi! This is such an awesome tutorial (and so much better than using HTML save that everyone else recommends). I was wondering if you could help me with the widget I made, it doesn’t seem to “refresh.” Any suggestions?
Yeah that happens sometimes try adding an empty commit to the page. If it didn’t work send me the link to your github repo I’ll check it out
Hi, first of all: wow. I have been trying to do this for like an hour, this was the last thing I was going to try, thank you so much!
Also, maybe a silly question, but I’m new to GitHub and was wondering: if I plan to use Github for other things in future in other repositories, since I published this as a site, will anyone be able to access any of my other private files somehow through this? Just a bit paranoid about it, thank you again!
You’re more than welcome!
If your repos are private then no one can access them. You’re public repos, on the other hand, can be easily found because the link to the widget will contain your Github username. If you don’t feel comfortable with that you might just create a different account for your widgets.
Hey, I can’t publish my widget since I don’t find the “GitHub Pages” in my GitHub settings. Can you help me with this??
Email me a screenshot of your settings at contact@shorouk.dev maybe I can help
Great tutorial! Very easy to follow and love how aesthetic the widget is. Keep up the good work, sir.